
A closed-loop relay test scheme was proposed in which identifies directly the crossover frequency (the frequency at which the loop gain is equal to 1). Other points on the Nyquist curve can be identified using a relay with hysteresis or by introducing an adjustable time delay in the closed-loop system.
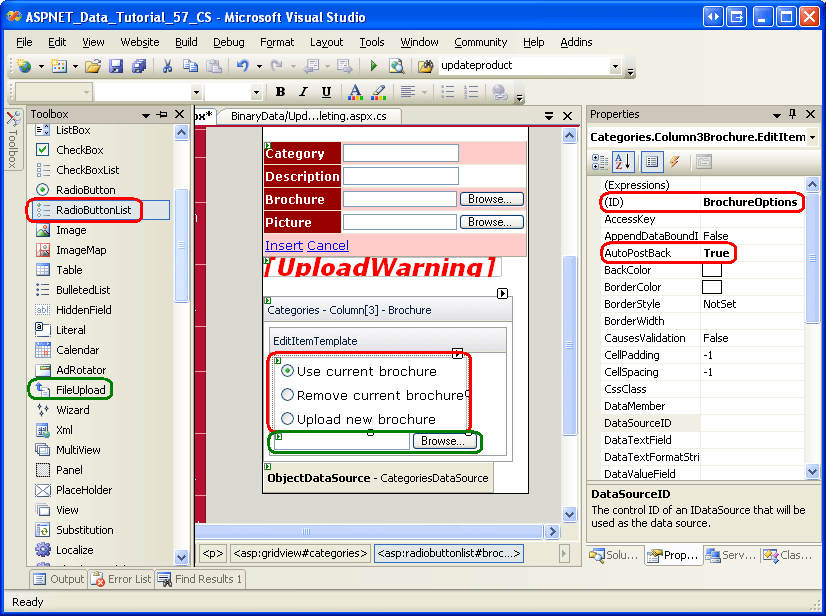
In 1984, Åström and Hägglund proposed an automatic tuning method based on a simple relay feedback test which gives, using the describing function analysis, the critical gain and the critical frequency of the system. In addition, they do not lead to on-line tuning methods in order to meet the specifications for The main drawback of these approaches is that the desired specifications are not necessarily achieved on the real system because of the approximations in modeling and/or equations. More advanced methods try either to find a solution by numerical methods or to simplify the equations using some approximations to find an analytic solution. The traditional methods are the graphical algorithms using Bode plots which are not very suitable for autotuning of the PID controllers. This problem, in general, even if the plant model is perfectly known, leads to a set of nonlinear equations for which no analytic solution is available. The specifications are often expressed in terms of phase and/or gain margins –, because they are the classical measures of robustness and together with the crossover frequency, they represent the time domain performance of the closed-loop system as well.
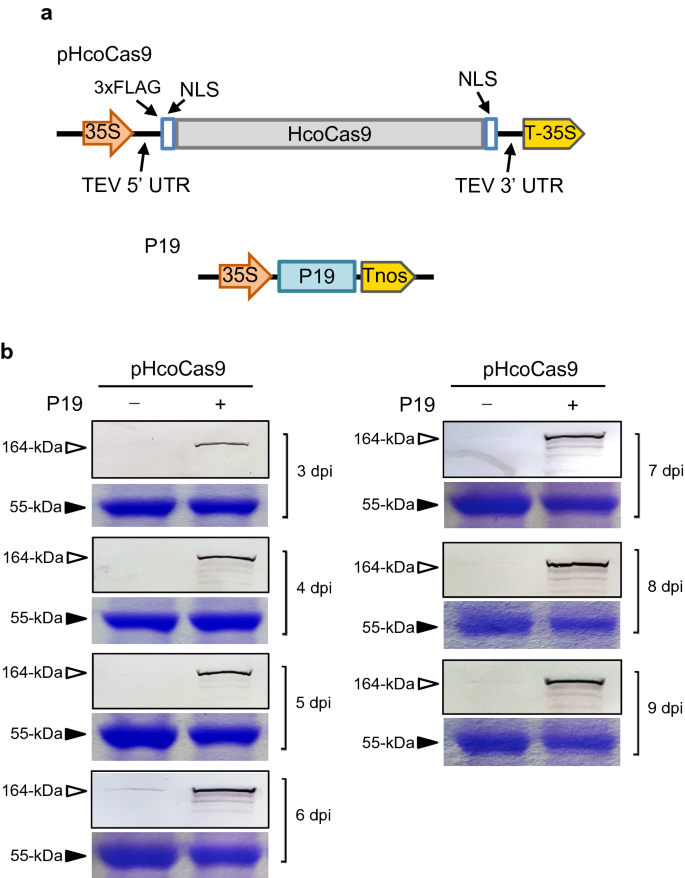
The available methods are normally based on a first or a second-order model with time delay obtained from the time response or the measurement of multiple points on the frequency response of the process. PID controllers are widely used in industrial plants and different methods for the design or the tuning of these controllers have been proposed in the literature –. Index Terms- Autotuning, iterative methods, proportional control, relay control system, robustness. Simulation examples and experimental results illustrate the effectiveness and the simplicity of the proposed method to design and tune the PID controllers. The method benefits from specific feedback relay tests to determine the gain margin, the phase margin and the crossover frequency of the closed-loop system.
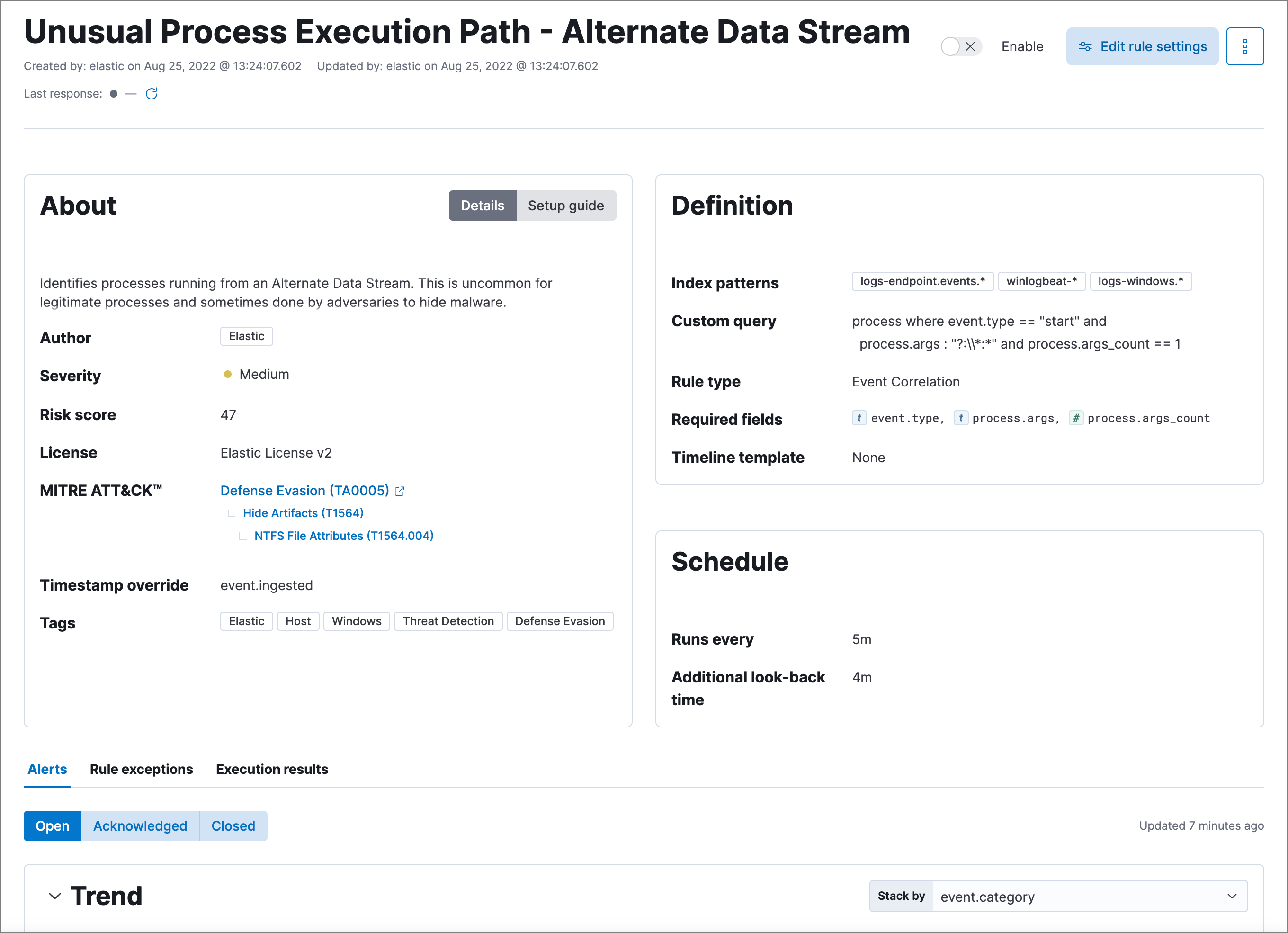

The frequency criterion is defined as the sum of squared errors between the desired and measured gain margin, phase margin and crossover frequency. Besides, the derivatives can be also employed to estimate the gradient and the Hessian of a frequency criterion in an iterative PID controller tuning method. This information can be used to design a PID controller for slope adjustment of the Nyquist diagram and improve the closed-loop performance. It is shown that the derivatives of amplitude and phase of a plant model with respect to frequency can be approximated by Bode’s integrals without any model of the plant. Abstract- A new method for PID controller tuning based on Bode’s integrals is proposed.


 0 kommentar(er)
0 kommentar(er)
